¶ Konzepte zur Ableitung von Ungewissheiten
¶ Generelle Herangehensweise
Folgende generelle Herangehensweise hat sich als günstig für die Ableitung von Ungewissheiten in komplexen Anwendungsfällen wie einem Endlager für hochradioaktive Abfälle erwiesen:
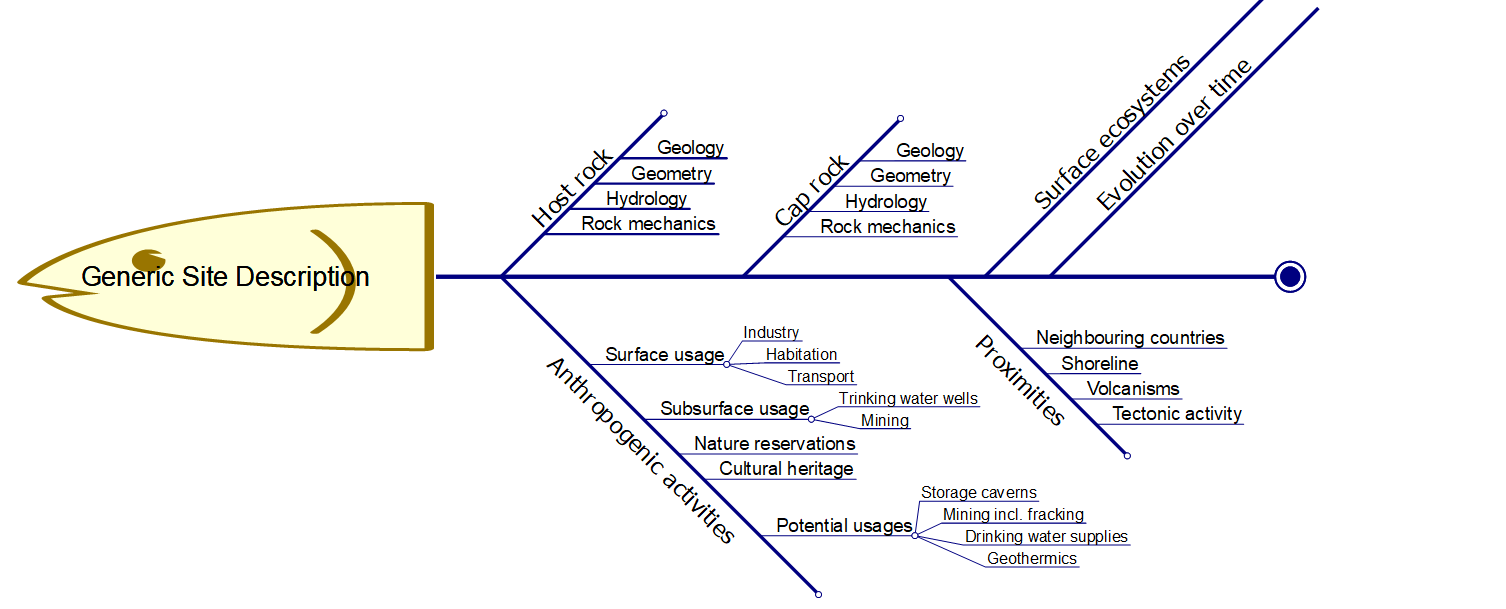
- Erfassung aller wesentlichen Modellparameter, zu denen Ungewissheiten bekannt sind, gemessen oder anderweitig bestimmt, oder abgeschätzt werden können. Für die Ermittlung von Abhängigkeiten von Parametern (und damit deren Ungewissheiten) sowie ihrer Visualisierung werden dabei häufig Tabellen genutzt. Die ISO empfiehlt in ihrem “Guide to the Expression of Uncertainty in Measurement - GUM” (International Organization for Standardization, 2008) sogenannte Fischgräten-Diagramme (auch als Ishigawa-Diagramme bezeichnet), welche Ursache-Wirkung-Beziehungen klar veranschaulichen kann, ein Beispiel ist in Abb. 1 gegeben.
- Quantifizierung der Ungewissheiten, d.h. welche Wahrscheinlichkeitsdichtefunktionen[1] (pdf: probability density function) nutzt man üblicherweise, was sind Alternativen zu pdfs? Spezialfälle sind hier die Ableitung von Ungewissheiten, wenn der Parameter selbst schon eine Schätzung ist. Im Rahmen verschiedener Projekte wie z.B. EURAD DONUT WP, Task 4 - "Tools and methods to quantify/derive uncertainties induce by coupled processes", NUMSA "Optimierung der numerischen Effizienz von Verfahren zur Sensitivitätsanalyse im Hinblick auf Modelle zur Analyse der Langzeitsicherheit von Endlagern" (Kuhlmann et al., 2013), „Uncertainties and Robustness with regard to the Safety of a repository for high-level radioactive waste – URS“ (Kurgyis et al., 2024) sowie mittels der Softwareplattform RESUS (Li, 2015) werden Unsicherheits- und Sensitivitätsanalysen und Wahrscheinlichkeitsdichtefunktionen für eine Vielzahl von physikalisch-chemischen Prozessen innerhalb des THMCb Konzepts (thermisch-hydraulisch-mechanisch-chemisch-mikrobiologisch gekoppelte Prozesse) geliefert, welche im Nah- und Fernfeld eines nuklearen Endlagers relevant sind. Dies wird von der Entwicklung entsprechender robuster Modelle begleitet.
- Einsatz der pdfs (oder anderer Repräsentationen von Ungewissheiten) in der Fehlerfortpflanzung, in Unsicherheits- und Sensitivitätsanalysen (siehe etwa Buchwald et al., 2024 im Kontext von THM Analysen von URL Versuchen).
- Ableitung von Konsequenzen aus der mathematischen Verarbeitung von Ungewissheiten: für die Interpretation der Sinnhaftigkeiten von Aussagen, der Streubreite von Zielwerten, Möglichkeiten zur Reduzierung von Ungewissheiten etc. (siehe bspw. Kiszkurno et al., 2024 für eine Anwendung in Bezug auf Modellselektion).
Es gibt eine Reihe etablierter Verfahren, je nach Fachgebiet, wie man Parameterungewissheiten behandelt. So sind in allen bisher erschienenen Bände der Thermochemical Database der NEA (NEA TDB) sehr umfassende Verfahren zur Berechnung von Ungewissheiten von abgeleiteten thermodynamischen Daten bei der Kombination mehrerer unabhängiger Quellen von Parameterwerten enthalten. Das Gleiche gilt für die neueste PSI/Nagra-TDB (Hummel & Thoenen, 2023), welche bei der Behandlung von Ungewissheiten Ansätze der NEA TDB weiterentwickelt hat. Die zu Grunde liegenden Annahmen und Prozeduren sind leicht auf nicht-geochemische Anwendungsfelder übertragbar. Nachfolgend ist als ein Anwendungsbeispiel ein ganzheitlicher Ansatz aus dem Bereich der Geochemie dargestellt.
Probabilistische Ansätze setzen die Kenntnis aller Quellen von Unsicherheiten voraus, um realistische Schätzwerte zu liefern (Bárdossy & Fodor, 2004). Sie werden genutzt, wenn Ungewissheiten in den Modellen als numerische Werte oder Wahrscheinlichkeitsverteilungen angegeben werden können. Worst-Case-Analysen (Morgan & Henrion, 1990) werden empfohlen, wenn nur obere und untere Schranken für Parameter vorhanden sind, vor allem wenn eine explizite Formulierung im Modell nicht umsetzbar ist. Hier werden Ungewissheiten oft durch einen sogenannten “best estimate” (realistischen) und pessimistischen (konservativen) Wert ausgedrückt. Angemerkt sei an dieser Stelle, dass die Worst-Case-Parametrisierung von Modellen nicht offensichtlich sein kann, da in vielen Modellen komplexe Wechselwirkungen zwischen physikalischen Prozessen zu stark nichtlinearen Interaktionen führen. Die Identifikation der ungünstigsten Parametrisierung kann also ebenso umfangreiche Variationen erfordern.
¶ Anwendungsbeispiels für UA / SA
¶ Für den Radionuklidtransport
Im Bereich potentieller Endlager für radioaktive Abfälle existieren bereits Konzepte, die Ungewissheiten, die durch veränderte geochemische Bedingungen hervorgerufen werden, adressieren. Ein Beispiel dafür ist das smart Kd-Konzept, wo wichtige geochemische Einflussgrößen wie pH-Wert, Ionenstärke, Konkurrenzkationen (z.B. Ca2+, Al3+) und komplexbildende Liganden (z.B. HCO3-, SO42-), welche die Retardation von Radionukliden bestimmen, identifiziert und in reaktiven Transportrechnungen berücksichtigt werden (Stockmann et al. 2017). Durch Koppelung eines statistischen Auswerteprogrammes, wie z.B. SimLab (JRC Ispra) mit einem geochemischen Speziationscode, wie z.B. PHREEQC (Parkhurst & Appelo, 2013) und UCODE (Poeter et al. 2014) als Interface zur Parametervariation steht eine Toolbox zur Verfügung, die Unsicherheits- und Sensitivitätsanalysen durchführen kann. Dies gestattet eine effiziente Zuweisung von Ressourcen zur Gewinnung der notwendigen physiko-chemischen Datenbasis mittels Feldanalysen und experimenteller Laborarbeiten. Das parallel dazu erlangte verbesserte Prozess- und Systemverständnis (mehrskalig von der atomaren Ebene bis zur technologischen Dimension) unterstützt eine sichere Auslegung von Endlagersystemen in tiefen Geosystemen.
¶ Für Barriereintegritätsuntersuchungen
Ungewissheiten in mechanischen, hydraulischen und thermischen Eigenschaften wirken sich auf die Ergebnisse THM-gekoppelter Simulationen aus, die der Bewertung der Integrität geotechnischer oder geologischer Barrieren dienen. Die Verknüpfung statistischer Werkzeuge wie etwa pyDOE2, GPy, statsmodels oder SALib aus dem Python-Ökosystem mit Simulationscodes für Prozessanalysen wie OpenGeoSys ermöglichen entsprechende Analysen ohne Eingriffe in die Prozesscodes selbst (nicht-intrusive Ansätze). In umfangreichen Sensitivitätsanalysen können wesentliche Parameter und Prozesskopplungen identifiziert werden (Chaudhry et al., 2021). Die so identifizierten Parameter- oder Parametergruppen sind somit von besonderer Relevanz mit Blick auf quantitative Bewertungen der Barriereintegrität und können unter Verwendung probabilistischer Konzepte zur Abschätzung von Ungewissheiten derjenigen Zielindikatoren dienen, aus denen Aussagen zur Beanspruchung der Barrieren abgeleitet werden (Buchwald et al., 2020; Plua et al., 2021).
Zurück zum vorherigen Thema Weiter zum nächsten Thema
[1] Können (transformierte) Gauß-Verteilungen sein, aber oft muss man auf einfachere, robustere pdfs ausweichen, wie z.B. Trigonale Verteilungen oder Gleichverteilung
¶ Referenzen
- Bárdossy, G., Fodor, J. (2004). Evaluation of uncertainties and risks in geology: new mathematical approaches for their handling (1st ed.). Springer Berlin, Heidelberg, New York, ISBN: 978-3-642-05833-2, 221pp
- Buchwald, J., Chaudhry, A. A., Yoshioka, K., Kolditz, O., Attinger, S., Nagel, T. (2020). DoE-based history matching for probabilistic uncertainty quantification of thermo-hydro-mechanical processes around heat sources in clay rocks. International Journal of Rock Mechanics and Mining Sciences, 134, 104481. DOI: 10.1016/j.ijrmms.2020.104481
- Buchwald, J., Kolditz, O., Nagel, T. (2024). Design-of-Experiment (DoE) based history matching for probabilistic integrity analysis — A case study of the FE-experiment at Mont Terri. Reliability Engineering & System Safety 244, 109903. DOI: 10.1016/j.ress.2023.109903
- Chaudhry, A. A., Buchwald, J., Nagel, T. (2021). Local and global spatio-temporal sensitivity analysis of thermal consolidation around a point heat source. International Journal of Rock Mechanics and Mining Sciences, 139, 104662. DOI: 10.1016/j.ijrmms.2021.104662
- Hummel, W., Thoenen, T. (2023). The PSI Chemical Thermodynamic Database 2020. Nagra Technical Report NTB 21-03, Wettingen, Switzerland, 1411pp, https://nagra.ch/wp-content/uploads/2023/05/NTB-21-03.pdf
- International Organization for Standardization (2008). Uncertainty of Measurement–Part 3: Guide to the expression of Uncertainty in Measurement (GUM: 1995). ISO. https://www.iso.org/standard/50461.html
- Kiszkurno, F.K., Buchwald, J., Kolditz, O., Nagel, T. (2024). Is more always better? Study on uncertainties introduced by decision-making process of model design and thermos-osmosis. Submitted to International Journal of Rock Mechanics and Mining Sciences
- Kuhlmann, S., Plischke, E., Röhlig, K.-J., Becker, D.-A. (2013). Sensitivity analysis: Theory and practical application in safety cases. The Safety Case for Deep Geological Disposal of Radioactive Waste: 2013 State of the Art. Symposium Proceedings of NEA/RWM/R. Paris, France. 7-9 October 2013. www.oecd-nea.org/rwm/docs/2013/rwm-r2013-9.pdf
- Kurgyis, K., Achtziger-Zupančič, P., Bjorge, M., Boxberg, M. S., Broggi, M., Buchwald, J., Ernst, O. G., Flügge, J., Ganopolski, A., Graf, T., Kortenbruck, P., Kowalski, J., Kreye, P., Kukla, P., Mayr, S., Miro, S., Nagel, T., Nowak, W., Oladyshkin, S., Renz, A., Rienäcker-Burschil, J., Röhlig, K.-J., Sträter, O., Thiedau, J., Wagner, F., Wellmann, F., Wengler, M., Wolf, J., Rühaak, W. (2024). Uncertainties and robustness with regard to the safety of a repository for high-level radioactive waste: introduction of a research initiative. Environmental Earth Sciences 83, 82. DOI: 10.1007/s12665-023-11346-8
- Li, X. (2015). Entwicklung der Softwareplattform RESUS: Repository Simulation, Uncertainty Propagation and Sensitivity Analysis. Dissertation, Clausthal, Press: Papier Flieger, Germany, ISBN: 978-3-86948-497-6, 185pp
- Morgan, M. G., Henrion, M. (1990). Uncertainty. Cambridge University Press. ISBN: 978-0-521-36542-0, 332pp
- Parkhurst, D.L., Appelo, C.A.J. (2013). Description of input and examples for PHREEQC version 3—A computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations: U.S. Geological Survey Techniques and Methods, book 6, chap. A43, 497 pp., U.S. Geological Survey, Denver, Colorado, http://pubs.usgs.gov/tm/06/a43
- Plúa, C., Vu, M. N., Armand, G., Rutqvist, J., Birkholzer, J., Xu, H., Guo, R., Thatcher, K. E., Bond, A. E., Wang, W., Nagel, T., Shao, H., & Kolditz, O. (2021). A reliable numerical analysis for large-scale modelling of a high-level radioactive waste repository in the Callovo-Oxfordian claystone. International Journal of Rock Mechanics and Mining Sciences, 140, 104574. DOI: 10.1016/j.ijrmms.2020.104574
- Poeter, E. P., Hill, M. C., Lu, D., Tiedeman, C. R., Mehl, S. (2014). UCODE_2014, with New Capabilities to Define Parameters Unique to Predictions, Calculate Weights using Simulated Values, Estimate Parameters with SVD, Evaluate Uncertainty with MCMC, and More. Integrated Groundwater Modeling Center Report GWMI 2014-02. Center of the Colorado School of Mines.
- Stockmann, M., Schikora, J., Becker, D.-A., Flügge, J., Noseck, U., Brendler, V. (2017). Smart Kd-values, their uncertainties and sensitivities - Applying a new approach for realistic distribution coefficients in geochemical modeling of complex systems. Chemosphere 187, 277–285, DOI: 10.1016/j.chemosphere.2017.08.115