¶ Datenlücken und -konsistenz
¶ Umgang mit Datenlücken
Eine Datenbasis kann nie vollumfänglich die thermodynamischen Daten aller denkbaren Reaktionen von aquatischen Spezies und Festphasen umfassen. Dies ist auch nicht generell notwendig. Kritische Datenlücken lassen sich neben neuen experimentellen Programmen zur Generierung der thermodynamischen Daten auch durch verschiedene Schätzmethoden schließen. Dabei kann über Sensitivitäts- und Unsicherheitsanalysen die Wirkung der dann im Regelfall größeren Ungewissheiten bestimmt werden.
- Das „Hard & Soft Acid & Base“-Konzept (HASB) basiert auf dem Lewis-Säuren/Basen-Prinzip auf und ermöglicht es, die Stabilität von Verbindungen bzw. deren Reaktivität abzuschätzen (Pearson, 1963; Railsback, 2007).
- Chemische Analogien zwischen chemischen Elementen mit gleichen Eigenschaften lassen sich ausnutzen, um Datenlücken zu schließen, z.B. können thermodynamischen Daten von aquatischen Spezies und Festphasen von dreiwertigen Lanthaniden und Actiniden (speziell Americium und Curium) übertragen werden (Neck et al., 2009). Ähnliches gilt im Falle von Oberflächenreaktionen für Minerale. Weitere Näherungen (Shock et al., 1997; Shock & Helgeson, 1988) beruhen auf Korrelationen im Helgeson-Kirkham-Flowers (HKF)-Modell (Helgeson et al., 1981).
- Die Lineare-Freie-Energie-Beziehung (Linear Free Energy Relationship - LFER) kann genutzt werden, um die Reaktionskonstante bzw. freie Gibbs-Energie einer gesuchten Reaktion abzuschätzen, indem für eine Reihe von vergleichbaren chemischen Reaktionen die Gleichgewichtskonstanten bzw. Gibbs-Energien in Beziehung gesetzt werden (McNaught et al., 1997). Besonders hervorzuheben ist dabei die Sverjensky-Mølling-Gleichung (Sverjensky et al., 1992, beispielhaft angewandt in Xu et al., 1999). Anwendungen aus dem Bereich der Sorption finden sich z.B. in (Bradbury & Baeyens, 2005).
- Bei den sogenannten Inkrementen-Modellen werden thermodynamische Eigenschaften von Festkörpern aus deren kristallographischen Grundbausteinen abgeleitet, siehe z.B. (Chen et al., 1999).
- Isocoulombische Ansätze: Für chemische Reaktionen, bei denen sich die Anzahl der Landungsträger nicht ändert, sog. isocoulombische Reaktionen, können gesuchte thermodynamische Daten durch Verwendung bekannter thermodynamischer Daten anderer, ebenfalls isocoulombischer Reaktionen abgeleitet werden. Zudem ist es dadurch möglich, die Temperaturabhängigkeit der Reaktion zu betrachten (Miron et al., 2020).
- Eine spezielle Art von Datenlücke ist das Fehlen von Temperaturabhängigkeiten. Neben der Nutzung von verschiedenen Vereinfachungen der van’t Hoff-Gleichung können auch isocoulombische Reaktionen eingesetzt werden. Alternativ bieten sich die DQuant-Gleichung (Helgeson, 1967) oder das Gleichungssystem nach Ryzhenko-Bryzgalin (Ryzhenko et al., 1985) an.
Zusätzlich soll hier noch auf eine Reihe von Fachzeitschriften explizit hingewiesen werden, welche regelmäßig thermodynamische Daten publizieren, also erste Anlaufpunkte beim Schließen entsprechender Lücken sein sollten. Diese sind insbesondere:
- Journal of Physical Chemistry Reference Data,
- Journal of Chemical Thermodynamics,
- Journal of Solution Chemistry,
- Journal of Physical Chemistry,
- Journal of Chemical and Engineering Data,
- Pure and Applied Chemistry,
- sowie Calphad - Computer Coupling of Phase Diagrams and Thermochemistry.
¶ Datenkonsistenz
¶ Interne Konsistenz
Es ist wichtig, dass Qualitätsanforderungen während des letzten Schritts der Zusammenführung von Daten aus verschiedenen Quellen ebenso gründlich berücksichtigt werden wie während der vorangegangenen Schritte (experimentelle Untersuchungen, Verarbeitung experimenteller Daten, Überprüfung und Zusammenstellung von Literaturdaten usw.). Das Konzept der internen Konsistenz ist dabei eine von mehreren Qualitätsanforderungen, quasi auf gleicher Relevanz-Ebene wie Genauigkeit und Vollständigkeit. Zwei Datenbanken, die in sich konsistent sind, können zueinander inkonsistent sein, und eine Datenbank, die aus zwei oder mehreren solchen Datenbanken abgeleitet ist, muss selbst in sich inkonsistent sein. Alle diese Kriterien müssen jedoch gleichzeitig berücksichtigt werden. Eine gute Einführung in diese Problematik bietet (Arthur, 2001).
Die interne Konsistenz wird durch Kriterien definiert, die für Entwicklung und Pflege thermodynamischer Datenbanken essentiell sind. Eine (unvollständige) Liste von Anforderungen lässt sich aus verschiedenen Publikationen ableiten, wie z.B. (CODATA, 1982; Nordstrom et al., 1990; oder Engi, 1992):
- alle Daten einer TDB sind mit den grundlegenden thermodynamischen Beziehungen kompatibel,
- alle Daten sind von einem Satz von Referenzwerten (Referenztemperatur Tr,, Referenzdruck pr, aber auch thermodynamische Werte für grundlegende Referenzspezies) und Konstanten (Gaskonstante, Molekulargewichte usw.) abgeleitet,
- es wurden geeignete Standardzustände gewählt und auf alle ähnlichen Stoffe angewandt,
- es wurde ein geeignetes mathematisches Modell gewählt, um alle temperatur- und druckabhängigen Daten anzupassen,
- es wurden geeignete chemische Modelle gewählt, um alle Aktivitäten in Mischsystemen (Gase, wässrige Lösung, Mischkristalle, Legierungen etc.) zu berechnen,
- es wurden alle relevanten experimentellen Daten (unterschiedlichster Art) simultan berücksichtigt sowie Konflikte und Unstimmigkeiten zwischen experimentellen Messungen aufgelöst.
Aus den obigen Anforderungen leitet sich ab, dass die interne Konsistenz erst dann vollständig definiert ist, wenn für jedes dieser Kriterien weitere Entscheidungen getroffen und Methoden ausgewählt und eingehalten werden. Wichtig: interne Konsistenz muss erfüllt sein, bevor die Genauigkeit einer Datenbank bewertet werden kann.
In einem eher praktischen Sinne ist die interne Konsistenz vielleicht am besten als idealer Standard zu betrachten, der zwar angenähert, aber selten voll erreicht wird (Engi, 1992). Eine Ursache ist das in Realität immer wieder notwendige Update von TDBs, um Ergebnisse neuer experimenteller Arbeiten einzupflegen. Die enge gegenseitige Abhängigkeit der Daten bedeutet dann mitunter, dass wesentliche Teile der TDB überarbeitet werden müssen, wenn auch nur ein einziger neuer Wert einer wichtigen Spezies eingegeben wurde.
Eine Voraussetzung für interne Datenkonsistenz ist somit der Aufbau auf einheitlich definierten fundamentalen physikalischen Konstanten, hier ist die CODATA der international anerkannte Standard (CODATA, 1986).
¶ Umrechnung der thermodynamischen Daten
Thermodynamische Daten lassen sich gemäß bekannter physikalisch-chemischer Gesetzmäßigkeiten ineinander umrechnen (Abb. 1).
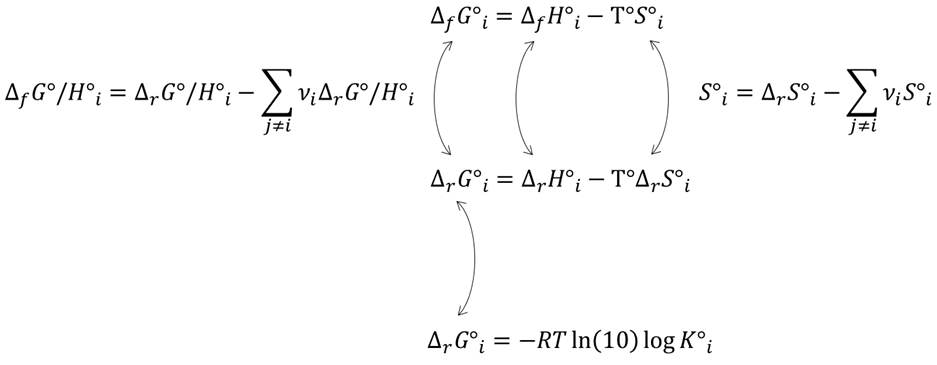
Neben der Umrechnung ist auch die Berechnung von Standarddaten (T = 298.15 K, p = 100 kPa, unendliche Verdünnung) ausgehend von parametrisierten Temperaturfunktionen möglich. Die Temperaturfunktionen stellen dabei eine polynome Beschreibung der Abhängigkeit des betrachteten Datentyps von der Temperatur dar. Basierend auf Betrachtungen von (Maier & Kelley, 1932), erweiterten (Haas & Fisher, 1976), das Konzept zur Temperaturabhängigkeit enthalpischer Größen von vier auf sechs Terme, welches momentan die am häufigsten genutzte Formulierung ist und auch von der NEA TDB (Grenthe et al., 2020) für die Temperaturabhängigkeit der Wärmekapazität genutzt wird:
$$H^0_T = H^0_{298} + a + bT + cT^2 + \frac{d}{T} + e \sqrt{T} + fT^3$$
Hierbei steht T für die Temperatur und H für die Enthalpie, "a-f" sind die konkreten Temperaturkoeffizienten. Eine weitere Methode, die Temperaturabhängigkeit einer chemischen Reaktion abzuschätzen, besteht in der Nutzung thermochemischer Größen (Enthalpie, Entropie und Wärmekapazität) als van’t-Hoff-Plot. Auch diese Beschreibungen der Temperaturabhängigkeiten lassen sich entsprechend physikalisch-chemischer Gesetzmäßigkeiten automatisiert ineinander umrechnen.
Durch diese Umrechnungsmöglichkeiten kann die Anzahl der zu speichernden Daten minimiert werden. Geeignete, direkt in das Datenbanksystem integrierte Prozeduren verringern zudem den Arbeitsaufwand für die Editoren eines Datenbankprojektes wie auch die Anzahl an Eingabe- bzw. Rechenfehlern. Gleichzeitig ergeben sich logische Ketten aufeinander aufbauender Abhängigkeiten, die sorgfältig beachtet und eingehalten werden müssen. Sollten sich Werte in diesen logischen Ketten ändern, erfordert dies zwingend eine Neu-Parametrisierung der darauf aufbauenden „abhängigen“ Datensätze. Solche logischen Abhängigkeiten sollten bereits bei der Eingabe neuer thermodynamischer Größen dahingehend berücksichtigt werden, dass Standarddaten von Reaktionspartnern so verwendet werden, dass eine nachträgliche Umrechnung im Idealfalle nicht nötig ist oder durch Prozeduren innerhalb der Datenbank automatisiert durchgeführt werden kann. In ungünstigen Fällen kann die Auswahl ungeeigneter Basis-Spezies bei der nachfolgenden Eingabe davon abhängiger Produktspezies eine Vielzahl von Umrechnungen erforderlich machen. Eine gesicherte konsistente Datenbehandlung kann z.B. durch die Implementierung von Sets verhindert werden: Gruppen von Datensätzen, die aufeinander aufbauen oder als in sich konsistent betrachtet werden. Dann ist es möglich, bei einer potenziell kritischen Änderung zurückzuverfolgen, welche Datensätze betroffen sind und dies für den Editor der Datensätze anzuzeigen (Moog et al, 2015).
Die Datenkonsistenz betrifft ebenso modellspezifische Wechselwirkungsparameter (SIT-, Pitzer-Parameter). Werden einer bestehenden Datenbasis weitere Daten (neue Spezies oder weitere Wechselwirkungsparameter) hinzugefügt, welche bei der Parametrisierung des originalen Datenbestandes nicht vorgesehen waren, wird im Regelfall die Gesamtaktivität aller aquatischen Spezies eines Elements überhöht berechnet. Dies wiederum hat Auswirkungen auf berechnete Löslichkeiten. Vom unqualifizierten Vereinigen mehrere Datensätze kann daher nur abgeraten werden.
Zurück zum vorherigen Thema Weiter zum nächsten Thema
¶ Referenzen
- Arthur, R.C. (2001). A Comment on the Internal Consistency of Thermodynamic Databases Supporting Repository Safety Assessments SKI Report 01:46
- Bradbury, M.H., Baeyens, B. (2005). Modelling the sorption of Mn(II), Co(II), Ni(II), Zn(II), Cd(II), Eu(III), Am(III), Sn(IV), Th(IV), Np(V) and U(VI) on montmorillonite: Linear free energy relationships and estimates of surface binding constants for some selected heavy metals and actinides. Geochim. Cosmochim. Acta 69, 875-892. DOI: 10.1016/j.gca.2004.07.020
- Chen, F., Ewing, R.C., Clark, S.B. (1999). The Gibbs free energies and enthalpies of formation of U6+ phases: An empirical method of prediction. Am. Mineralogist 84, 650-664. DOI: 10.2138/am-1999-0418
- CODATA (1982). A systematic approach to the preparation of thermodynamic tables. Report of the CODATA task group on internationalization and systematization of thermodynamic tables. CODATA Bull., 47, 13pp
- CODATA (1986). The 1986 adjustment of the fundamental physical constants. A report of the CODATA Task Group on Fundamental Constants, prepared by Cohen, E. R. & Taylor, B. N., Tech. Rep. 63
- Engi, M. (1992). Thermodynamic data for minerals: a critical assessment. In: The stability of minerals (G.D. Price and N.L. Ross, eds.), Chapman & Hall, London, 267-328
- Haas Jr., J.L., Fisher, J.B. (1976). Simultaneous evaluation and correlation of thermodynamic data. Am. J. Sci. 276, 525-545. DOI: 10.2475/ajs.276.4.525
- Helgeson, H.C. (1967). Thermodynamics of complex dissociation in aqueous solutions at elevated temperatures. J. Phys. Chem. 71, 3121-3136. DOI: 10.1021/j100869a002
- Helgeson, A.C., Kirkham, D.A. Flowers, G.C. (1981). Theoretical prediction of the thermodynamic behavior of aqueous electrolytes at high pressure and temperature: IV. Calculations of activity coefficients, osmotic coefficients and apparent molal and standard and relative partial molal properties to 600°C and 5 KB. Am. J. Science 281, 1249–1516. DOI: 10.2475/ajs.281.10.1249
- Maier, C.G., Kelley, K.K. (1932). An Equation for the Representation of High-Temperature Heat Content Data. J. Am. Chem. Soc. 54, 3243–3246. DOI: 10.1021/ja01347a029
- McNaught, D., Wilkinson, A. (1997). IUPAC. Compendium of Chemical Terminology (the "Gold Book"). 2nd Ed., Blackwell Scientific Publications, Oxford. DOI: 10.1351/goldbook
- Miron, G.D., Kulik, D.A., Thoenen, T. (2020). Generating isocoulombic reactions as a tool for systematic evaluation of temperature trends of thermodynamic properties: Application to aquocomplexes of lanthanides and actinides. Geochim. Cosmochim. Acta 286, 119–142. DOI: 10.1016/j.gca.2020.07.020
- Moog, H., Bok, F., Marquardt, C.M., Brendler, V. (2015). Disposal of Nuclear Waste in Host Rock formations featuring high-saline solutions - Implementation of a Thermodynamic Reference Database (THEREDA). App. Geochem. 55, 72–84. DOI: 10.1016/j.apgeochem.2014.12.016
- Neck, V., Altmaier, M., Rabung, T., Fanghänel, T. (2009). Thermodynamics of trivalent actinides and neodymium in NaCl. MgCl2 and CaCl2 solutions: Solubility, hydrolysis and ternary Ca-M(III)-OH complexes. Pure Appl. Chem. 81, 1555-1568. DOI: 10.1351/PAC-CON-08-09-05
- Nordstrom, D.K., Plummer, L.N., Langmuir, D., Busenberg, E., May, H.M., Jones, B.F., Parkhurst, D.L. (1990). Revised chemical equilibrium data for major water-mineral reactions and their limitations. In. Chemical modeling of aqueous systems II (D.C. Melchior and R.L. Bassett, eds.). Am. Chem. Soc. Symp. Ser. 416, 399-413
- Pearson, R.G. (1963). Hard and Soft Acids and Bases. J. Am. Chem. Soc. 85, 3533–3539. DOI: 10.1021/ja00905a001
- Railsback, L.B. (2007). Patterns in the compositions of oxysalt and sulfosalt minerals, and the paradoxical nature of quartz. Am. Mineral. 92, 356-369. DOI: 10.2138/am.2007.2310
- Ryzhenko, B.N., Bryzgalin, O.V., Artamkina, I.Y., Spasennykh, M., Shapkin, A.I. (1985). An electrostatic model for the electrolytic dissociation of inorganic substances dissolved in water. Geochem. Internat. 22, 138-144
- Shock, E.L., Helgeson, H.C. (1988). Calculation of the thermodynamic and transport properties of aqueous species at high pressures and temperatures: correlation algorithms for ionic species and equation of state predictions to 5 kb and 1000°C. Geochim. Cosmochim. Acta 52, 2009–2036. DOI: 10.1016/0016-7037(88)90181-0
- Shock, E.L., Sassani, D.C., Willis, M., Sverjensky, D.A. (1997). Inorganic species in geologic fluids: correlations among standard molal thermodynamic properties of aqueous ions and hydroxide complexes. Geochim. Cosmochim. Acta 61, 907–950. DOI: 10.1016/s0016-7037(96)00339-0
- Sverjensky, D.A., Molling, P. (1992). A linear free energy relationship for crystalline solids and aqueous ions. Nature 356, 231-234. DOI: 10.1038/356231a0
- Xu, H., Wang, Y., Barton, L.L. (1999). Application of a linear free energy relationship to crystalline solids of MO2 and M(OH)4. J. Nucl. Mater. 273, 343-346. DOI: 10.1016/S0022-3115(99)00092-6